$\vec{w}h\alpha\mathfrak{t}\;\; i\mathbb{S}\ldots$
the $\mathsf P$ versus $\mathsf{NP}$ problem?
Before the BMS Friday Colloquium by Prof. Susanne Albers
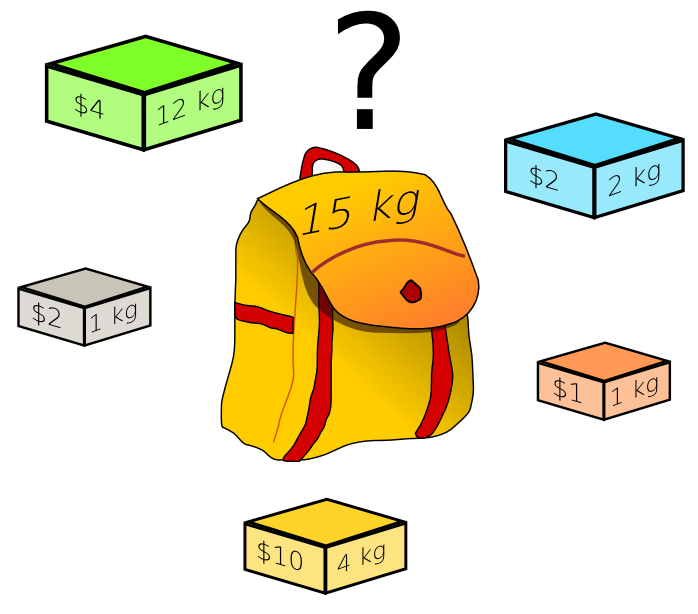
Which boxes in the picture above should be chosen to maximize the amount of money while still keeping the overall weight under or equal to 15 kg? Problems of this type are called knapsack problems. They belong to the class of $\mathsf{NP}$ problems, which are in general very hard to solve.
Let $\mathsf P$ be the class of problems that can be solved in polynomial time. $\mathsf P$ is a subset of $\mathsf{NP}$. One of the Millenium problems is to decide whether $\mathsf P$ equals $\mathsf{NP}$. Put differently, we want to know if there are problems whose answer can be quickly checked, but which require an impossibly long time to solve even on a supercomputer.
We will define the classes $\mathsf P$ and $\mathsf{NP}$ using Turing machines, give plenty of examples and explain why the $\mathsf P$ vs. $\mathsf{NP}$ problem is important.
(CC BY-NC 2.5) xkcd.com (by Randall Munroe)